What expectation values are reachable via autonomous unitary dynamics?

If you take a pure quantum state $\ket\psi$ and consider its orbit under Hamiltonian dynamics $\ket{\psi(t)} = \exp(-iHt) \ket\psi$, what range of expectation values can it take (for some fixed observable $X$)? The problem boils down to maximization (or reliable method of approximation) of $\langle X \rangle$ over the orbit – that is, one needs to find

\begin{equation}\begin{aligned} \sup_{t\in \mathbb{R}} \bra{\psi(t)} X \ket{\psi(t)}. \end{aligned} \end{equation}

First, let us solve a considerably simpler problem of rank-1 observables: if $\ket\phi$ is fixed, then the expectation value of $X=\ket\phi\bra\phi$ is the overlap (squared) between the evolving state $\ket{\psi(t)}$ and $\ket\phi$:

\begin{equation}\begin{aligned} \langle X \rangle_{\psi(t)} = \vert\langle \phi \vert \psi(t)\rangle\vert^2. \end{aligned} \end{equation}

Then, maximization of such $X$ is equivalent to finding the maximal possible overlap $\vert\langle \phi \vert \psi(t)\rangle\vert^2$. And this is a relatively simple problem, with the additional assumption that $H$ has nondegenerate eigenspaces (to eigenenergies $E_k$), and the vector of phase factors $(\exp(-iE_k t))$ can approximate any phase structure1. This is so because both $\ket\psi$ and $\ket\phi$ can be decomposed in the eigenbasis ${\ket{k}}$; let's assume that

\begin{equation}\begin{aligned} \ket\psi &= \sum_k \sqrt{p_k} \ket{k},\\ \ket\phi& = \sum_k \sqrt{q_k} \exp(i\alpha_k).\end{aligned} \end{equation}

The phase factors in $\ket\psi$ can be made trivial by proper choice of the eigenvectors - the differential phase $\exp(i\alpha_k)$ is what matters anyway.

With this assumptions, the differential phase can be negated to arbitary degree by the unitary evolution. In such a case in the following equation the final inequality becomes equality.

\begin{equation}\begin{aligned} \sup_{t\in \mathbb{R}}\vert\langle \phi \vert \psi(t)\rangle\vert^2 = \lvert \sum_k \sqrt{p_k q_k} e^{-i(\alpha_k+E_k t)} \rvert^2 \le \lvert\sum_k \sqrt{p_k q_k}\rvert^2. \end{aligned} \end{equation}

Then, $\sup_t \langle X \rangle_{\psi(t)}=\lvert\sum_k \sqrt{p_k q_k}\rvert^2$ depends on the eigendecomposition of $\ket\psi$ and $\ket\phi$, and has a closed form. But what can be done for more complex (non-projective) operators $X$?

Fejer-Riesz theorem and semidefinite optimization

Let's write the expectation value of $X$ over $\ket{\psi(t)}$ explicitly in the eigenbasis of $H$:

\begin{equation}\begin{aligned} \langle X \rangle_{\psi(t)} = \sum_{k,k'} X_{k,k'} \sqrt{p_{k'} p_k} \exp\left(i(E_k-E_{k'})t\right). \end{aligned}\end{equation}

With $z:=\exp(it)$, the phase terms can be written as $z^{E_k-E_{k'}}$. With a bit of notation abuse, the expectation value can be then reinterpreted as a sum over energy differences $\kappa = E_k-E_{k'}$ (for each $k$ and $k'$):2

\begin{equation}\begin{aligned} \langle X \rangle_{\psi(t)} = \sum_{\kappa} M_\kappa z^\kappa. \end{aligned}\end{equation}

This almost looks like a trigonometric polynomial – and indeed it is, if all energy differences $\kappa$ are natural numbers. This is rarely the case, but (after rescaling the Hamiltonian $H$) it might be a reasonable approximation. Importantly, one can find maxima of trigonometric polynomials over unit circle with semidefinite optimization, and I thought that maybe the approximations may be controlled to yield better and better results.

Better approximations increase the overall degree of the trigonometric polynomial. In the infinite degree limit, one can relax the problem3 to a workable semidefinite optimization instance — and surprisingly, the dual problem encodes exactly the constraints expected in quantum mechanics. This dual problem is:

\begin{equation}\begin{aligned} \max_{\rho} \quad & \Tr(\rho X), \\ \text{s.t.}\quad & \rho\succcurlyeq 0, \\ & \Tr \rho=1, \\ & \Tr H^n \rho = \langle H^n\rangle_\psi. \\ \end{aligned}\end{equation}

The moment-matching constraints are exactly what can be produced via Hamiltonian evolution with $H$ – of course the energy $\langle H\rangle$ is conserved, but this holds also for the second moment $\langle H^2\rangle$, and in general $\langle H^n\rangle_\psi = \langle H^n\rangle_{\psi(t)}$. The relaxation to mixed states $\rho$ becomes a semidefinite optimization instance – it's just maximization of $\langle X \rangle_\rho$ over a specific spectrahedron.

One would expect that the relaxed semidefinite problem finds a suboptimal state, yielding an upper bound to maximal achievable $\langle X \rangle_{\psi(t)}$. However, often the resulting $\rho$ is pure – and theoretically 4 there exist pure states $\exp(-i Ht)\ket{\psi}$ arbitrarily close to it.

Example

Consider the following qutrit operators:

\begin{equation}\begin{aligned} X &= \left( \begin{array}{ccc} 0 & \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & 0 \\ \end{array} \right),\\ Y&=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right). \end{aligned}\end{equation}

The question is: what is the set of all possible expectation values $(\langle X\rangle, \langle Y\rangle)$ for all qutrit states? And, given a Hamiltonian $H$ and an initial state $\ket\psi$, how to construct the set of reachable expectation values $(\langle X\rangle, \langle Y\rangle)_{\psi(t)}$?

For $\ket\psi=(1,0,0)^T$ and

\begin{equation}\begin{aligned} H&=\left( \begin{array}{ccc} 0 & 1 & i \\ 1 & 0 & 1 \\ -i & 1 & 1 \\ \end{array} \right), \end{aligned}\end{equation}

the result is following:

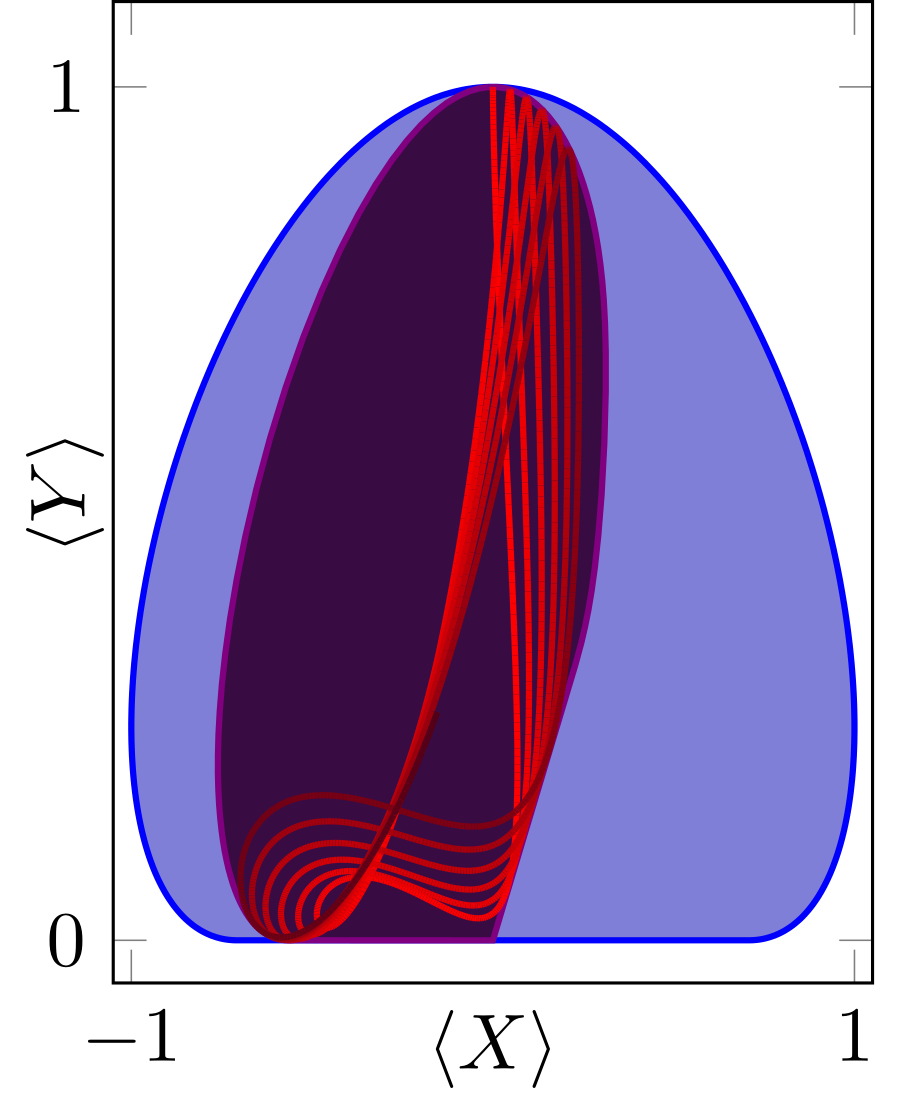
Here, the unconstrained set of possible expectation values is shown in blue; the shadow of the orbit $\exp(-iH t) \ket\psi$ is shown as a red curve, and the set of possible correlations achievable with this dynamics is shown in purple – it is determined using the method sketched above, without the need to calculate the orbits to infinity.5

  1. That is: for arbitary $(\exp(i\alpha_k))_k$, and $\varepsilon>0$, one can find $t\in\mathbb{R}$ such that $ \sum_k \lvert \exp(i\alpha_k) - \exp(-iE_k t)\rvert $ is smaller than $\varepsilon$. ↩

  2. Here, $M_\kappa$ is a sum of all terms $X_{k,k'} \sqrt{p_k p_{k'}}$ over all pair $(k,k')$ such that $E_k-E_{k'}=\kappa$. ↩

  3. By demanding that numbers on each sub/superdiagonal are equal. ↩

  4. If, as previously, any arbitrary phase structure can be reached with $H$ – there are no hidden resonances in the energy structure. ↩

  5. For each $(n_x,n_y)\in\RR^2$, state $\rho_*$ maximizing $\langle n_X X+n_Y Y\rangle_\rho$ with the constraints $\langle H^n\rangle_\rho = \langle H^n\rangle_{\psi}$ is determined. The tuple of expectation values $(\langle X\rangle_{\rho_*}, \langle Y\rangle_{\rho_*})$ is calculated – it lies in the boundary of the purple set shown in the picture. The entire boundary is approximated by sampling sufficiently many distinct vectors $(n_X, n_Y)$. ↩