Quantum Information Geometry

Quantum mechanics primer

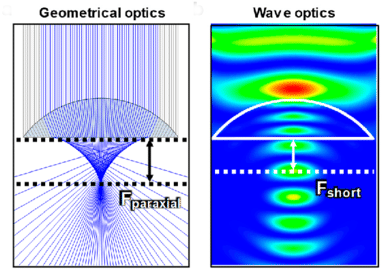
Lee, G. J. et al., Micromachines 2020.

• Einstein: light is photons — 'wave components', each with definite energy and wavelength.
• de Broglie: … maybe electrons are similar? (yes!)
• Schrödinger: insight from the limit
  wave optics \(\rightarrow\) ray optics, `electron wave' described by \(\psi(x,y,z,t)\), \[i \frac{\partial \psi}{\partial t} \!=\! \overbrace{\left(\!-(\partial^2_x\!+\!\partial^2_y\!+\!\partial^2_z)\!+\!\frac{k}{\sqrt{x^2\!+\!y^2\!+\!z^2}}\!\right)}^{H} \psi\]
• Quantum information: restricted linear subspaces of $\psi$:\[\psi = c_1 \psi_1 +\ldots+c_d \psi_d.\]

What is measurement?

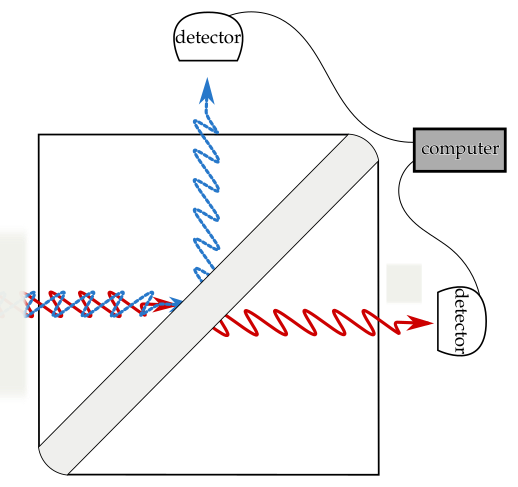
• Coupling between the system and the outside world: \[i\frac{\partial \psi}{\partial t} = (H_{\text{sys}}\otimes\operatorname{Id} + \operatorname{Id}\otimes H_{{world}} + H_{\text{int}} ) \psi\]
• Macroscopically different: clear interpretation!
• Result (in the simplest case): \(\exists\) orthonormal bases \(\color{blue}\{e_i\}\) and \(\color{green}\{f_j\}\) such that \[\left.\psi\right|_{t=0}=\left(\sum {\color{red}c_k}{\color{blue}e_k} \right)\otimes w \mapsto\sum {\color{red}c_k} {\color{blue}e_k} \otimes {\color{green}f_k} =: \left. \psi\right|_{t\rightarrow \infty}\]
• Born interpretation: probability \(\propto~\)norm\(^2=\lvert {\color{red}c_k}\rvert^2\) .
• We don't know the details!

What is measurement?

• Observations are discrete, single observation \(\approx\) element of the basis \(\{e_k\}\). Often an eigenbasis of some physically relevant operator \(A\): \[A=\sum \lambda_k \Pi_{e_k}.\] (\(A\) self-adjoint, real eigenvalues.)
• `Moments of \(A\)' inferred from observation statistics. Expectation value: \[E(A) = \braket{v, Av} \color{gray} =\sum_k \frac{n_k}{\sum_j n_j} \lambda_k.\]

State vectors are not the entire story

Mixed states

• What if the black box generates \(v_k\) according to the ensemble \(\{(p_k,v_k)\}\)?
• Expectation value linear: \[\sum p_k \braket{v_k,A v_k}=\operatorname{Tr} A \overbrace{\sum p_k \Pi_{v_k}}^{\rho}\]
• Definition (mixed states of dimension \(d\)): \[\mathcal{M_d} = \{ \rho \in M_{d\times d} : \rho=\rho^\dagger, \operatorname{Tr} \rho=1, \rho \succeq 0\}.\]
• All properties defined by \(\rho\). Details of the ensemble do not matter!
• Tomography: reconstruction of \(\rho\) from measurement statistics.

Projections of mixed states

Definition (joint numerical range): \[W(A_1, \ldots, A_n) = \{ \vec x \in \mathbb{R}^n | \exists_v \braket{v,v}=1, \forall_i x_i = \braket{v, A_i v} \}\]

\(A_i\) self-adjoint: observations related to orthogonal eigenbases.

Joint numerical range of three \(3\times 3\) matrices

Left: KS, S. Weis, K. Życzkowski, Classification of joint numerical ranges of three hermitian matrices of size three, LAA 2018,
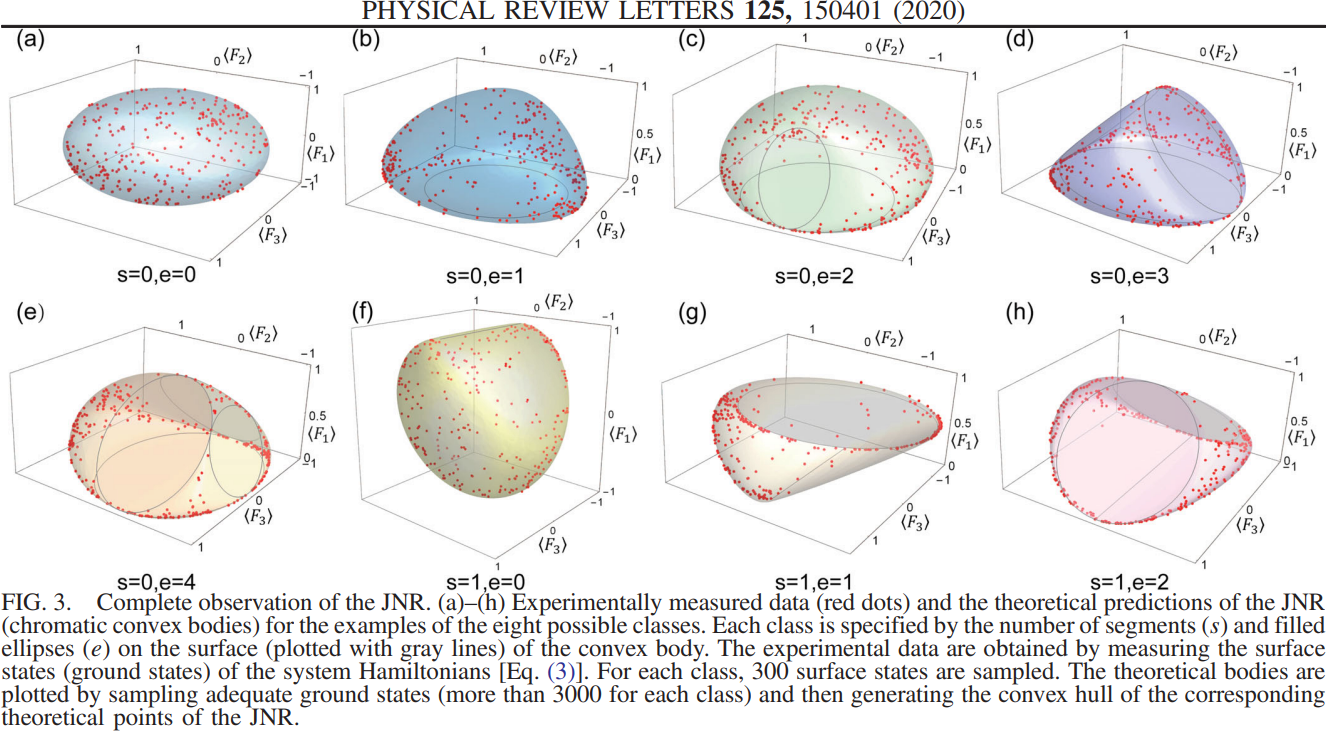
Top: J. Xie et al., Observing geometry of quantum states in a three-level system, PRL 2020.

Duality to spectrahedra and polynomial equations

Uncertainty relations

• Variance: also inferred from observation statistics, \[\operatorname{Var}(A)=E(A^2)-E(A)=\braket{v,A^2 v}-\braket{v,Av}^2.\]
• Given two measurements $A$ and $B$, what is the relation between variances?
• The Heisenberg uncertainty relation: \[\operatorname{Var}(X) \operatorname{Var}(P) \ge \frac14,\] for \(X\) and \(P\) being linear operators \((X v)(x,y,z)=x v(x,y,z), (P v)(x,y,z) = -i\left.\frac{\partial}{\partial x}v\right|_{x,y,z}\)

Sum of variances: 3D joint numerical range

With \((x,x')~\in~W(X,X^2),\) \(\operatorname{Var}(X)=x'-x^2.\)

\[(x,y,z) \in W(X,Y,X^2+Y^2):\] \[\operatorname{Var}(X)+\operatorname{Var}(Y)=z-x^2-y^2.\]

Lemma: minimal sum on variances attained on the surface of \(W(X,Y,X^2+Y^2)\), tangent to the paraboloid of revolution.

Result: This defines a system of polynomial equations. Could be solved for physically relevant case generators of \(SU(2)\) representation.

Summary

• Quadratic forms in quantum mechanics define expectation values.
• Numerical ranges are sets of possible tuples of them.
• Useful in study of uncertainty relations and entanglement. (among others)
• Multiple open problems!

Thank you for your attention!

References:

1. K.S., Numerical ranges and geometry in quantum information: Entanglement, uncertainty relations, phase transitions, and state interconversion (PhD thesis), arXiv: 2303.07390,
2. K.S., S. Weis, K. Życzkowski, Classification of joint numerical ranges of three hermitian matrices of size three, LAA 2018,
3. T. Simnacher, J. Czartowski, K.S., K. Życzkowski, Confident entanglement detection via the separable numerical range, PRA 2021,
4. K.S., K. Życzkowski, Geometric and algebraic origins of additive uncertainty relations, J Phys A 2019,
5. Lee, G. J. et al., Micromachines 2020.
6. J. Xie et al., PRL 2020

Correlation between different parts of the system

• State of two systems: \(\rho\in \mathcal{M}_{d_1\times d_2}\)
  (\(\rho=\) convex combination of projectors onto subspaces in \(\mathcal{H}_{d_1}\otimes\mathcal{H}_{d_2} \))
• No correlation at all: \(\rho = \rho' \otimes \rho''\)
• Any non-tensor \(\rho\): correlation when measuring two subsystems!
• Definition (separable states of bipartite \(\mathcal{H}_{d_1}\otimes\mathcal{H}_{d_2}\)): \[ \mathcal{M}^{\text{sep}}_{d_1,d_2} = \operatorname{conv}\{ \Pi_{v_k'}\otimes \Pi_{v_k''}: v'\in\mathcal{H}_{d_1}, v''\in\mathcal{H}_{d_2}\} \]
• \(\mathcal{M}^{\text{sep}}_{d_1,d_2}\) allows for correlations… but not all of them!
  

  \(\mathcal{M}^{\text{sep}}_{d_1,d_2}\) is a proper convex subset of \(\mathcal{M}_{d_1\times d_2}\).

Entanglement and separable numerical ranges

Joint numerical range vs separable numerical range

• \(W_{\text{sep}}=\{\vec a \in \mathbb{R}^n | a_i = \operatorname{Tr} \rho A_i, \rho \in \mathcal{M}^{\text{sep}}\}\)
• Expectation values outside \(W_{\text{sep}}~\implies\) entanglement!
• \(W_{\text{sep}}\) convex \(\implies\) defined by linear constraints.
• Approximation by half-space intersection in general NP-hard!
  S. Friedland, L-H. Lim, Nuclear Norm of Higher-Order Tensors, Math. Comp. 2014

Entanglement and separable numerical ranges

Goal: maximize \(\operatorname{Tr} X(\rho'\otimes \rho'')\) over \( \rho'\in\mathcal{M}_2, \rho''\in\mathcal{M}_d \).

Lemma: Optimization reduces to finding a point on the surface of 4D joint numerical range, tangent to a hypercone.

Main points:

• \( \operatorname{Tr} X (\rho'\otimes \rho'')=\operatorname{Tr} \rho' X''\), where \[X''=\operatorname{Tr}_2 X (\operatorname{Id} \otimes \rho'')\]
• For \(\rho''\) fixed, \[\max_{\rho'} \operatorname{Tr} \rho' X'' = \lambda_{\max}(X'').\]
• \(X'' \in M_{2\times 2} \implies \) for \(X_i=\operatorname{Tr}_1 X(\sigma_i\otimes \operatorname{Id})\), \[\lambda_{\max}(X'')=x_0+\sqrt{x_1^2+x_2^2+x_3^2}\]
• Linearization possible: then semidefinite programming.

\(\operatorname{Tr}_2\): linear extension of \[\operatorname{Tr}_2 A \otimes B = A \operatorname{Tr} B.\] Similarly, \[\operatorname{Tr}_1 A \otimes B=B \operatorname{Tr} A.\]